Advection tests

Advection tests are a good tool to understand the effects of both amplitude and phase errors of a numerical scheme. A high order temporal scheme reduces amplitude errors (1st and 2nd order schemes have positive amplitude errors, and 3rd and 4th order schemes have weakly negative amplitude errors). The phase error, on the other hand, is reduced by high order spatial schemes. Nevertheless, in a step function the highest wavenumber contributions always suffer an error. In an advection test those highest wavenumber contributions will propagate too slowly, and this is what leads to the well-known Gibbs phenomenon.



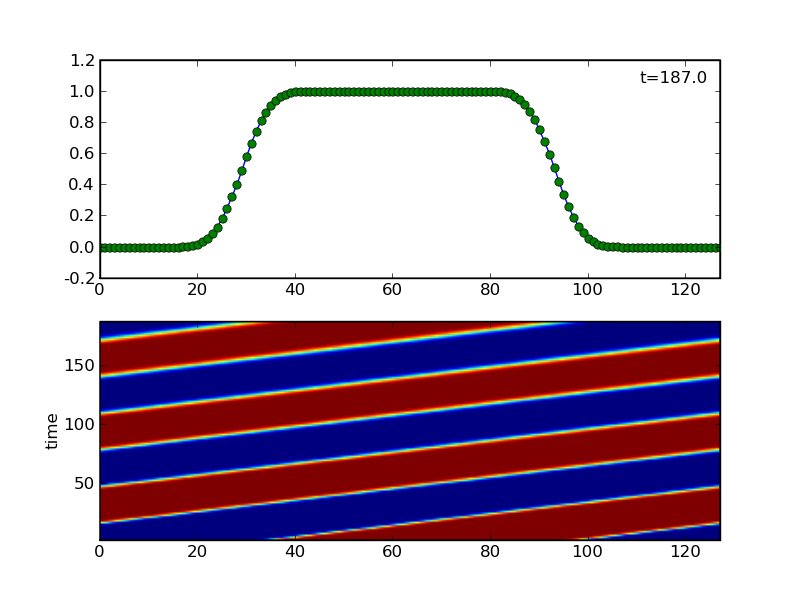
In this test we used "widthcc=.1" in start.in and "pscalar_diff=1e-4" with "cdt=0.8" in run.in.

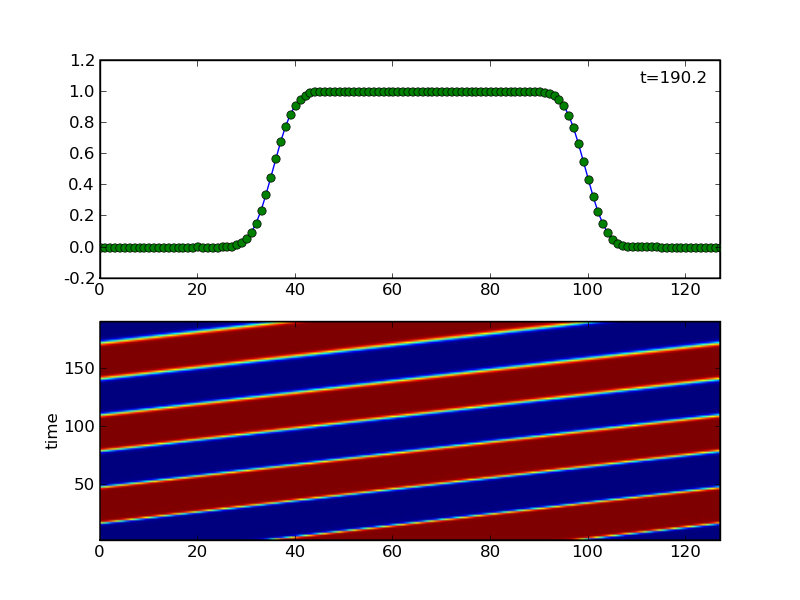
In this test we also used "widthcc=.1" in start.in, but now with "pscalar_diff=5e-5" and "cdt=0.4" in run.in.

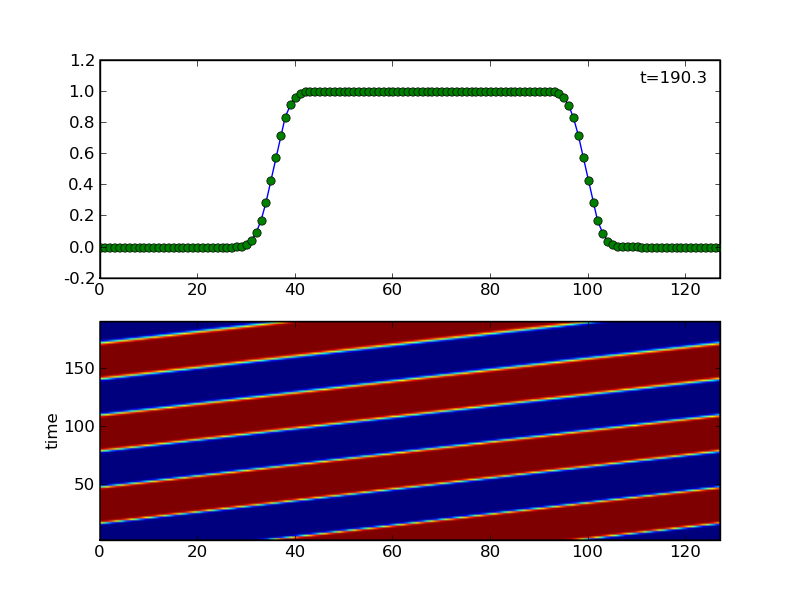
Same as above, but with a 10th order scheme using "pscalar_diff=2e-5" and again "cdt=0.4" in run.in.


Numerical Experiments homepage



---

$Date: 2009/09/22 06:33:36 $, $Author: brandenb $, $Revision: 1.8 $