Recent research highlights

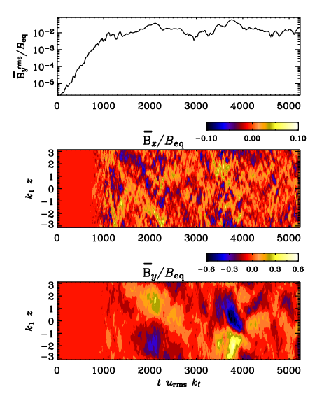
	Large-scale fields from shear-flow turbulence compatible with incoherent alpha-shear dynamo shear-current dynamo not excited shown with test-field method all components of diffusion tensor obtained				Brandenburg, A., Rädler, K.-H., Rheinhardt, M., & Käpylä, P. J.: 2008, ``Magnetic diffusivity tensor and dynamo effects in rotating and shearing turbulence,'' Astrophys. J. 676, 740-751 (arXiv:0710.4059, ADS, PDF) citations 125 on ADS, 137 on Google Scholar
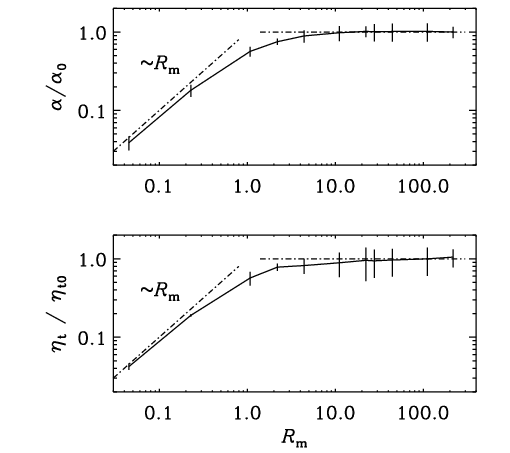
	Kinematic alpha effect in isotropic turbulence simulations test-field method applied to isotropic turbulence shows that turb. diffusion ηt=⅓τu2rms. and τ=(urmskf)-1 to good approximation				Sur, S., Brandenburg, A., & Subramanian, K.: 2008, ``Kinematic alpha effect in isotropic turbulence simulations,'' Monthly Notices Roy. Astron. Soc. 385, L15-L19 (arXiv:0711.3789, ADS, PDF) citations 90 on ADS, 96 on Google Scholar
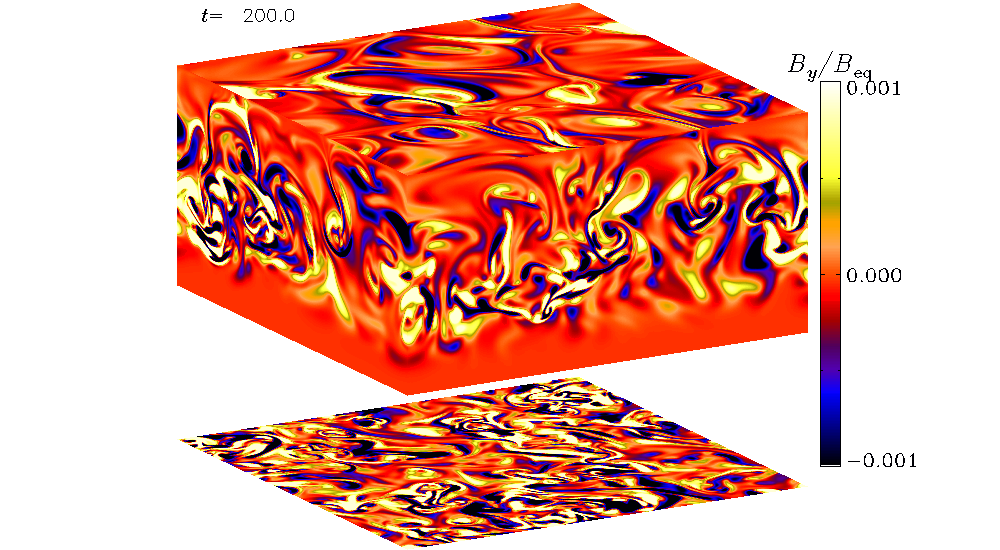
	Large-scale dynamos in turbulent convection with shear α-Ω type dynamos from convection Strong horizontally averaged fields Horizontal shear: drives magnetic helicity vertically Vertical shear: drives magnetic helicity horizontally Quenching alleviated by normal-field condition				Käpylä, P. J., Korpi, M. J., & Brandenburg, A.: 2008, ``Large-scale dynamos in turbulent convection with shear,'' Astron. Astrophys. 491, 353-362 (arXiv:0806.0375, ADS, PDF) citations 107 on ADS, 120 on Google Scholar
	Cyclic magnetic activity due to turbulent convection in spherical wedge geometry Convectively driven dynamo in spherical wedge produces long cycle periods (∼33 years) equatorward migration of toroidal flux belts Hossenfelder's blog entry about the Sun's butterfly diagram				Käpylä, P. J., Mantere, M. J., & Brandenburg, A.: 2012, ``Cyclic magnetic activity due to turbulent convection in spherical wedge geometry,'' Astrophys. J. Lett. 755, L22 (arXiv:1205.4719, ADS, DOI, PDF) citations 146 on ADS, 161 on Google Scholar
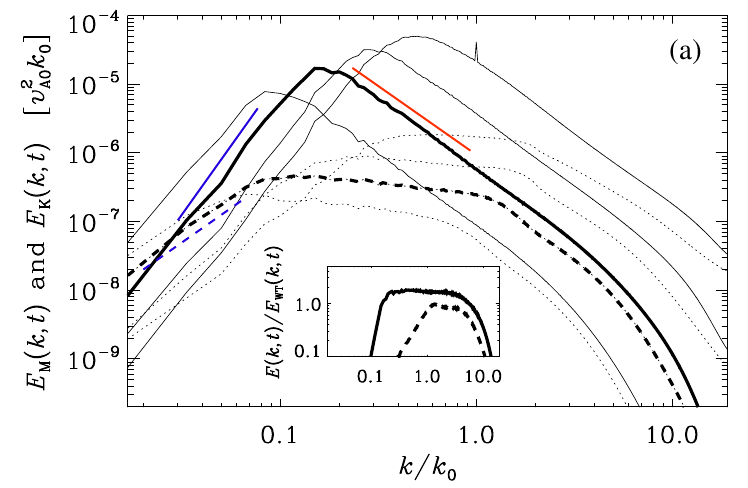
	Inverse transfer even for nonhelical turbulence Magnetically dominated turbulence Nonhelical inverse transfer possible k-2 inertial range spectrum Wave turbulence coefficient CWT=1.9				Brandenburg, A., Kahniashvili, T., & Tevzadze, A. G.: 2015, ``Nonhelical inverse transfer of a decaying turbulent magnetic field,'' Phys. Rev. Lett. 114, 075001 (arXiv:1404.2238, ADS, DOI, PDF, PDF) citations 107 on ADS, 95 on Google Scholar
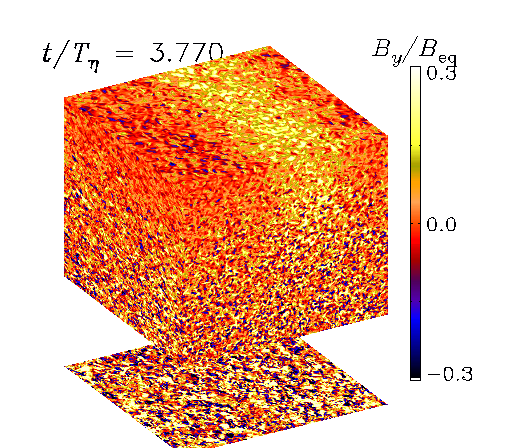
	Detection of negative effective magnetic pressure instability in simulations Conclusively demonstrates negative effective magnetic pressure instability(NEMPI) is caused by magnetic suppression of turbulent pressure reduction is stronger than added explicit pressure argued to be relevant to formation of active regions				Brandenburg, A., Kemel, K., Kleeorin, N., Mitra, D., & Rogachevskii, I.: 2011, ``Detection of negative effective magnetic pressure instability in turbulence simulations,'' Astrophys. J. Lett. 740, L50 (arXiv:1109.1270, ADS, DOI, HTML, PDF) citations 56 on ADS, 71 on Google Scholar
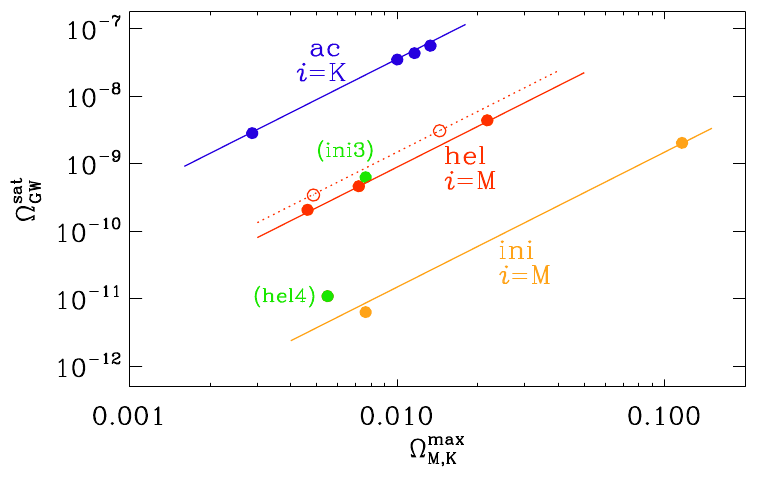
	Numerical Simulations of Gravitational Waves from Early-Universe Turbulence Strongest efficiency for acoustic turbulence Shallow low-frequency tail Sharp drop above driving frequency Same sign of GW circular polarization and magnetic helicity				Roper Pol, A., Mandal, S., Brandenburg, A., Kahniashvili, T., & Kosowsky, A.: 2020, ``Numerical Simulations of Gravitational Waves from Early-Universe Turbulence,'' Phys. Rev. D 102, 083512 (arXiv:1903.08585, ADS, DOI, HTML, PDF) citations 71 on ADS, 44 on Google Scholar